-
В закладки
 В закладки будет добавлено толкование к данному слову в данном словаре. Закладки сохраняются на Вашем компьютере в cookie. Если Ваш браузер не поддерживает cookie или такая возможность отключена, то сохранение закладок будет не возможно.
В закладки будет добавлено толкование к данному слову в данном словаре. Закладки сохраняются на Вашем компьютере в cookie. Если Ваш браузер не поддерживает cookie или такая возможность отключена, то сохранение закладок будет не возможно.эпициклоида
эпицикло́ида, -ы -
В закладки
 В закладки будет добавлено толкование к данному слову в данном словаре. Закладки сохраняются на Вашем компьютере в cookie. Если Ваш браузер не поддерживает cookie или такая возможность отключена, то сохранение закладок будет не возможно.
В закладки будет добавлено толкование к данному слову в данном словаре. Закладки сохраняются на Вашем компьютере в cookie. Если Ваш браузер не поддерживает cookie или такая возможность отключена, то сохранение закладок будет не возможно.Эпициклоида
ЭПИЦИКЛОИДА (от эпи... и Циклоида) - плоская кривая, описываемая точкой окружности, которая извне касается неподвижной окружности и катится по ней без скольжения. См. также Кардиоида, Циклоида, Гипоциклоида. -
В закладки
 В закладки будет добавлено толкование к данному слову в данном словаре. Закладки сохраняются на Вашем компьютере в cookie. Если Ваш браузер не поддерживает cookie или такая возможность отключена, то сохранение закладок будет не возможно.
В закладки будет добавлено толкование к данному слову в данном словаре. Закладки сохраняются на Вашем компьютере в cookie. Если Ваш браузер не поддерживает cookie или такая возможность отключена, то сохранение закладок будет не возможно.Эпициклоида
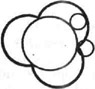
(от эпи... и циклоида), плоская кривая (рис.), описываемая точкой окружности, к-рая извне касается неподвижной окружности и катится по ней без скольжения. См. также Кардиоида, Циклоида, Гипоциклоида.
-
В закладки
 В закладки будет добавлено толкование к данному слову в данном словаре. Закладки сохраняются на Вашем компьютере в cookie. Если Ваш браузер не поддерживает cookie или такая возможность отключена, то сохранение закладок будет не возможно.
В закладки будет добавлено толкование к данному слову в данном словаре. Закладки сохраняются на Вашем компьютере в cookie. Если Ваш браузер не поддерживает cookie или такая возможность отключена, то сохранение закладок будет не возможно.Эпициклоида
- плоская кривая, траектория точки окружности, катящейся по другой окружности и имеющей с ней внешнее касание. Параметрич. уравнения:
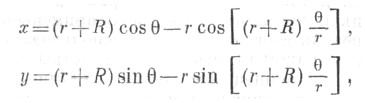
где r - радиус катящейся окружности, R - радиус неподвижной окружности,
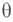 - угол, стягиваемый дугой между точками касания окружностей (см. рис.).
- угол, стягиваемый дугой между точками касания окружностей (см. рис.). 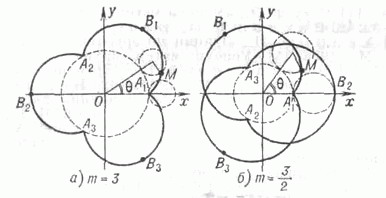
В зависимости от величины модуля m=R/r получаются Э. различной формы. При т=1Э.- кардиоида, при тцелом кривая состоит из тнепересекающихся ветвей. Точки возврата А 1, А2, . . .. А т имеют полярные координаты
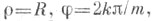 k=0,1, . . ., т-1. Вершины кривой B1, В2, . . ., В т имеют координаты
k=0,1, . . ., т-1. Вершины кривой B1, В2, . . ., В т имеют координаты 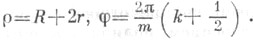 При тдробном ветви перекрещиваются; при тиррациональном число ветвей бесконечно, точка Мв исходное положение не возвращается; при
…
При тдробном ветви перекрещиваются; при тиррациональном число ветвей бесконечно, точка Мв исходное положение не возвращается; при
…
Далее
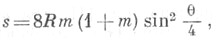 длина дуги от точки В 1:
длина дуги от точки В 1: 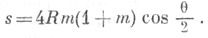 Площадь сектора, ограниченного двумя радиус-векторами кривой и дугой кривой:
Площадь сектора, ограниченного двумя радиус-векторами кривой и дугой кривой: 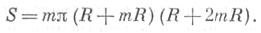 Радиус кривизны:
Радиус кривизны: