Поиск по словарю Математический словарь
-
В закладки
 В закладки будет добавлено толкование к данному слову в данном словаре. Закладки сохраняются на Вашем компьютере в cookie. Если Ваш браузер не поддерживает cookie или такая возможность отключена, то сохранение закладок будет не возможно.
В закладки будет добавлено толкование к данному слову в данном словаре. Закладки сохраняются на Вашем компьютере в cookie. Если Ваш браузер не поддерживает cookie или такая возможность отключена, то сохранение закладок будет не возможно.Аксиоматическая Теория Множеств
-направление в математич. логике, занимающееся изучением фрагментов содержательной теории множеств методами математич. логики. Обычно с этой целью фрагменты теории множеств оформляются в виде формальной аксиоматич. теории. В более узком смысле термин "А. т. м." может служить для обозначения к.-л. формальной аксиоматич. теории, направленной на построение нек-рого фрагмента содержательной ("наивной") теории множеств.
Теория множеств, возникшая на рубеже 19-20 вв., уже в самом начале своего развития натолкнулась на парадоксы. Открытие таких фундаментальных парадоксов, как Рассела и Кантора (см. Антиномия), вызвало широкую дискуссию и способствовало коренному пересмотру логико-математич. принципов. Аксиоматич. направление в теории множеств можно рассматривать как инструмент более детального изучения положения дел в создавшейся ситуации.
Построение формальной А. т. м. начинается с точного описания языка, на к-ром формулируются утверждения. Затем принципы "наивной" теории множеств выражаются на описанном языке в виде аксиом, схем аксиом. Ниже дано краткое описание нек-рых наиболее распространенных систем А. т. м. Важную роль при этом играет язык, содержащий следующие исходные символы: 1) переменные
 к-рые в языке играют роль общих имен множеств; 2) предикатные символы е (знак принадлежности) и = (знак равенства); 3) оператор дескрипции
к-рые в языке играют роль общих имен множеств; 2) предикатные символы е (знак принадлежности) и = (знак равенства); 3) оператор дескрипции 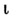 (означающий "такой объект, что..."); 4) логические связки и кванторы:
(означающий "такой объект, что..."); 4) логические связки и кванторы: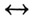 (эквивалентно),
(эквивалентно),  (влечет),
(влечет),  (или),
(или), 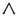 (и),
(и), 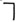 (не),
(не), 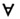 (для всех),
(для всех), (существует); 5) скобки ( , ). Выражения языка делятся на термы и формулы. Термы являются именами множеств, а формулы выражают суждения. Термы и формулы образуются согласно следующим правилам.
(существует); 5) скобки ( , ). Выражения языка делятся на термы и формулы. Термы являются именами множеств, а формулы выражают суждения. Термы и формулы образуются согласно следующим правилам. П1. Если
 - переменные или термы, то
- переменные или термы, то  и
и  суть формулы.
суть формулы. П2. Если Аи В - формулы и х - переменная, то
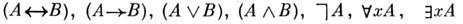 суть формулы и
суть формулы и  - терм; переменная хесть терм.
- терм; переменная хесть терм. Напр., формула
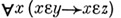 выражает суждение "уесть подмножество z", ее естественно обозначить
выражает суждение "уесть подмножество z", ее естественно обозначить  терм
терм  является именем множества всех подмножеств z, в привычной математич. символике его обозначают через Pz. Пусть знак
является именем множества всех подмножеств z, в привычной математич. символике его обозначают через Pz. Пусть знак  означает "стоящее слева есть обозначение для стоящего справа". Приведем нек-рые дальнейшие обозначения для формул и термов.
означает "стоящее слева есть обозначение для стоящего справа". Приведем нек-рые дальнейшие обозначения для формул и термов. Пустое множество:

Множество таких х, что (х).
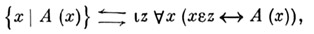
где z не входит свободно в (х).(т. е. не является параметром формулы (х)).
Неупорядоченная пара хи у.
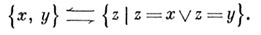
Одноэлементное множество из х:
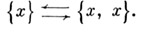
Упорядоченная пара хи у:

Объединение хи у:
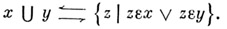
Пересечение хи у:

Объединение всех элементов х:

Декартово произведение х и у:
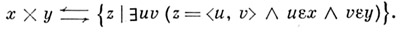
wесть функция:

Значение функции
 на элементе х:
на элементе х: 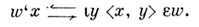
zесть стандартное бесконечное множество:
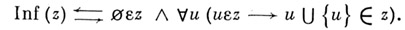
Следующая аксиоматич. теория А наиболее полно отражает принципы "наивной" теории множеств. Аксиомы А:
А1. аксиома объемности:
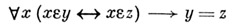
("если множества уи z содержат одни и те же элементы, то они равны");
А2. аксиомы свертывания:
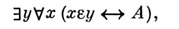
где А - произвольная формула, не содержащая в качестве параметра у("существует множество у, содержащее те и только те элементы х, для к-рых А").
Описанная система противоречива. Если в А2 в качестве Авзять формулу
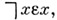 то из формулы
то из формулы 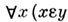
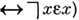 легко выводится
легко выводится  , что противоречиво.
, что противоречиво. Аксиоматич. системы теории множеств можно разделить на следующие четыре группы.
а) Построение аксиоматич. систем первой группы направлено на такое ограничение аксиом свертывания, к-рое обеспечивает наиболее естественный способ формализации обычных математич. доказательств и в то же время позволяет избежать известных парадоксов. Первой аксиоматикой такого рода была система Z Цермело (Е. Zermelo, 1908). Однако в системе Z невозможно естественным образом формализовать нек-рые разделы математики, и А. Френкель (A. Fraenkel, 1922) предложил пополнить Z новым принципом, названным им аксиомой подстановки. Полученная система наз. системой Цермело- Френкеля и обозначается ZF.
б) Вторую группу составляют системы, аксиомы к-рых выбраны в связи с к.-л. объяснением парадоксов, напр, как следствий непредикативных определений. Сюда относятся: разветвленная теория типов Рассела, простая теория типов Т, теории типов с трансфинитными индексами (см. Типов теория).
в) Третья группа характеризуется использованием нестандартных средств логич. вывода, многозначных логик, дополнительных условий на доказательства, бесконечных правил вывода. Системы, относящиеся к этому направлению, наименее развиты.
г) Четвертая группа включает модификации систем первых трех групп, преследующие определенные логич. или математич. цели. Укажем только на системы NBG Неймана - Гёделя - Бернайса (J. Neumann - К. Godel-Р. Bernays, 1925) и NF Куайна (W. Quine, 1937). Построение системы NBG вызвано желанием иметь конечное число аксиом для теории множеств, основанной на системе ZF. В NF реализуется стремление преодолеть расслоение понятий, имеющее место в теории типов.
Системы Z, ZF, NF можно формулировать в описанном выше языке. Правила вывода, а также так наз. логические аксиомы у этих систем совпадают и образуют прикладное исчисление предикатов 1-й ступени с равенством и оператором дескрипции. Укажем только аксиомы для равенства и оператора дескрипции:

где (х) - формула, не содержащая связанной переменной у(т. е. не имеющая вхождений вида
 iy), и (у).получается из формулы (х).заменой нек-рых свободных вхождений
iy), и (у).получается из формулы (х).заменой нек-рых свободных вхождений 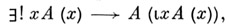 переменной хна у; где квантор
переменной хна у; где квантор 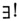 х означает "существует одно и только одно х", а формула
х означает "существует одно и только одно х", а формула  получается из формулы (х).заменой всех свободных вхождений переменной хна терм
получается из формулы (х).заменой всех свободных вхождений переменной хна терм  Квантор
Квантор 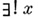 выразим через кванторы
выразим через кванторы 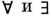 и равенство.
и равенство. Нелогические аксиомы системы Z:
Z1. аксиома объемности А1;
Z2. аксиома пары:
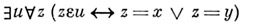
("существует множество {х, у}");Z3. аксиома суммы:

("существует множество
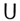 z"); Z4. аксиома степени:
z"); Z4. аксиома степени: 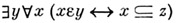
("существует множество Pz");Z5. аксиома выделения:

("существует подмножество z, состоящее из тех элементов х, для к-рых имеет место (х)");аксиомы Z2 -Z5 являются примерами аксиом свертывания; Z6. аксиома бесконечности:

Z7. аксиома выбора:

("для всякого множества
 существует функция
существует функция 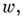 выбирающая из каждого непустого элемента хмножества z единственный элемент
выбирающая из каждого непустого элемента хмножества z единственный элемент  "). К этим аксиомам добавляют еще аксиому фундирования: Z8.
"). К этим аксиомам добавляют еще аксиому фундирования: Z8. 
цель к-рой - постулировать, что не существует убывающих цепей
 Аксиома Z8 позволяет упростить построения в Z. Добавление этой аксиомы не вносит противоречия.
Аксиома Z8 позволяет упростить построения в Z. Добавление этой аксиомы не вносит противоречия. В системе Z можно развивать арифметику, анализ, функциональный анализ, рассматривать кардинальные числа, меньшие
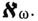 Однако если определить алефы стандартным образом, то доказать в Z существование
Однако если определить алефы стандартным образом, то доказать в Z существование  и более высоких кардиналов уже невозможно.
и более высоких кардиналов уже невозможно. Система ZF получается из Z добавлением аксиом подстановки Френкеля, к-рым можно придать вид аксиом свертывания:
ZF9.
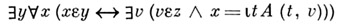
("существует множество у, состоящее из
 когда vпробегает все элементы множества z"). Иначе говоря, уполучается из z, если каждый элемент у из z заменить на
когда vпробегает все элементы множества z"). Иначе говоря, уполучается из z, если каждый элемент у из z заменить на 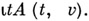
Система ZF является очень сильной теорией. Все обычные математич. теоремы формализуются в ZF.
Система NBG получается из системы ZF добавлением нового типа переменных - классовых переменных X, Y, Z, ... и конечного числа аксиом образования классов, позволяющих доказать формулы вида

где (х) - формула системы NBG, не содержащая связанных классовых переменных и символа i. Поскольку по каждой формуле (х).можно образовать класс, то бесконечное число аксиом ZF удается заменить конечным числом аксиом, содержащих классовую переменную. Аксиома выбора имеет вид:

и утверждает существование единой для всех множеств функции выбора, являющейся классом.
Система NF имеет наиболее простую аксиоматику, а именно: 1) аксиому объемности и 2) те аксиомы свертывания, в к-рых формулу Аможно стратифицировать, т. е. приписать всем переменным формулы Аверхние индексы таким образом, чтобы получилась формула теории типов Т, т. е. в подформулах вида хeуиндекс у хна единицу меньше, чем индекс у y.
Система NF обладает следующими особенностями:
а) выбора аксиома и обобщенная континуум-гипотеза опровержимы;
б) бесконечности аксиома доказуема;
в) аксиома объемности играет весьма существенную роль. Так, если аксиому объемности заменить несколько более слабой аксиомой:

допускающей много пустых множеств, а аксиомы свертывания NF оставить без изменения, то получится довольно слабая теория, именно: уже в формальной арифметике можно доказать непротиворечивость полученной системы.
Ниже приведены результаты о соотношениях между описанными системами.
(a) Всякая формула ZF доказуема в NBG тогда и только тогда, когда она доказуема в ZF.