Альтернативным кольцом (А. к.) наз. кольцо, в к-ром каждые два элемента порождают ассоциативное подкольцо; альтернативной алгеброй (А. а.) наз. линейная алгебра, являющаяся А. к. Согласно теореме Артина класс всех А. к. задается системой тождеств:

Таким образом, все А. к. составляют многообразие. Термин "А. к." оправдан тем, что в любом таком кольце ассоциатор (дефект ассоциативности)

является кососимметрической (альтернативной) функцией своих аргументов.

Первым примером А. к. явились Кэли числа, дающие пример альтернативного тела, т. е. А. к. с единицей, в к-ром однозначно разрешимы уравнения ах=b и уа=b для всех bи всех 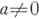. Альтернативные тела играют существенную роль в теории проективных плоскостей, поскольку проективная плоскость муфангова (т. е. плоскость трансляций относительно любой прямой) тогда и только тогда, когда любое координатизирующее ее тернарное кольцо является альтернативным телом. Если в кольце Rс единицей каждый элемент обратим, и для любых 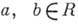выполняется тождество (или тождество то Rявляется альтернативным телом. Всякое альтернативное тело либо ассоциативно, либо имеет строение Кали - Диксона алгебры, над своим центром.

Всякое простое А. к. также либо ассоциативно, либо является алгеброй Кэли - Диксона над своим центром (последняя в этом случае не обязана уже быть телом). Алгебрами Кэли - Диксона исчерпываются за пределами ассоциативных и все примитивные А. к. Всякое первичное А. к. Л, если либо ассоциативно, либо является кольцом Кэлн - Диксона.

Многие свойства А. к. весьма сильно отличаются от свойств ассоциативного кольца в аналогичных ситуациях. Так, если Rесть А. к., а Аи В - его правые идеалы, то их произведение А В уже не обязано быть правым идеалом, даже если А - двусторонний идеал в R; но произведение двусторонних идеалов А. к. является его двусторонним идеалом. Различие в случае ассоциативных колец и А. к. сильно проявляется и в том, что в А. к. существуют различные нильпотентности, поскольку произведение элементов, при одной расстановке скобок равное 0, при другой - может быть отлично от 0. Обычно в А. к. используются следующие нильпотентности: разрешимость (кольцо Rназ. разрешимы м индекса т, если существует такое число т, что ),правая нильпотентность (существует такое число п, что где 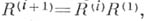и нильпотентность (существует такое число k, что т. е. произведение любых kэлементов Rравно 0 при любой расстановке скобок). Имеется А. к. разрешимое индекса 3, но не нильпотентное. Правая нильпотентность в А. к. эквивалентна нильпотентности (А. к., правонильпотентное индекса n, нильпотентно индекса 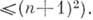Локально, т. е. на конечно порожденных кольцах, все нильпотентности эквивалентны. Теория, устанавливающая достаточные признаки локальной нильпотентности А. к., вполне параллельна соответствующей теории для ассоциативных колец. Это вытекает из следующего факта: пусть Rесть А. к., в к-ром можно выбрать такую систему Sпорождающих, что любые два элемента из Sпорождают нилькольцо; пусть, далее, все ассоциативные гомоморфные образы Rлокально нпль-потентны, тогда R локально нильпотентно. Поэтому если R есть А. к. с тождеством то R локально нильпотентно; если R есть А. а. с тождеством, к-рое не является следствием ассоциативности, и каждый элемент R есть сумма конечного числа нильэлементов, то алгебра R локально нильпотентна. Если речь идет не о локальной, а о глобальной нильпотентности, то ситуация в А. к. отличается от ассоциативной. Так, уже А. к. R с тождеством не обязано быть нильпотентным (даже если его аддитивная группа без кручения). Однако А. к. с тождеством и без элементов порядка в аддитивной группе разрешимо индекса Если R - алгебраич. А. а. с тождественным соотношением, не являющимся следствием ассоциативности (или степени алгебраичности элементов R ограничены в совокупности), то R локально конечномерна.

В А. к. имеется аналог Джекобсона радикала:во всяком А. к. R существует максимальный квазирегулярный идеал 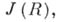равный пересечению всех модулярных максимальных правых идеалов. Факторкольцо является J-полупростым, т. е. J(R/J(R))=0; если I есть идеал всякое I-полупростое кольцо аппроксимируется примитивными А. к. (т. е. примитивными ассоциативными кольцами и алгебрами Кэли - Диксона). Имеются аналоги и всех других ассоциативных радикалов (нижнего нильрадикала, локально нильпотентного радикала и т. д.), к-рые обладают теми же основными свойствами, что и в ассоциативных кольцах.