- обобщение понятия аналитического многообразия. Локальной моделью (и одновременно важнейшим примером) аналитич. ространства над полным недискретно нормированным полем kявляется аналитическое множество в области 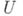n-мерного пространства над полем k, заданное уравнениями (где - аналитич. функции в U), к-рое снабжено пучком , получающимся при ограничении на пучка 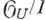, где - пучок ростков аналитич. функций в U, а I - подпучок идеалов, порожденный 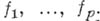Аналитическим пространством над k наз. окольцованное пространство, локально изоморфное окольцованному пространству указанного выше вида. Если k - поле действительных чисел , говорят о вещественных аналитических пространствах; если k - поле комплексных чисел 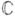, - о комплексных аналитических (просто комплексных) пространствах; если k - поле р-адических чисел 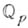, - о р- адических аналитических пространствах.

Аналитическим (голоморфным) отображением одного аналитич. ространства 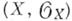в другое наз. морфизм в смысле теории окольцованных пространств, т. е. пара (, ), где : 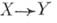- непрерывное отображение, a j₁. 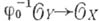-гомоморфизм пучков. Точка хА. п. 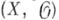наз. простой (или неособой), если хобладает окрестностью, над к-рой 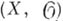изоморфно пространству вида , где - область в В противном случае хваз. особой точкой. Пространство наз. гладким, если все его точки просты. Гладкое аналитич. ространство - это не что иное, как аналитич. многообразие.

Размерность 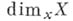А. п. X в точке определяется как размерность соответствующего аналитич. множества в локальной модели. Глобальная размерность определяется формулой

Пусть 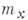- максимальный идеал в локальном кольце 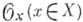. Векторное пространство над kназ. касательным пространством к в точке х, а 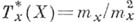- кокасательным пространством. Число

наз. касательной размерностью, пли размерностью вложения, в точке х(последнее наименование связано с тем, что является наименьшим из чисел птаких, что в окрестности точки изоморфно локальной модели в пространстве ). Размерность , причем равенство имеет место тогда и только тогда, когда х - простая точка. Определяется также размерность

Каждое аналитич. отображение А. п. : определяет линейное отооражение 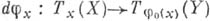, к-рое наз. его дифференциалом в точке 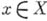А. п. наз. приведенным, если его локальная модель в окрестности любой точки обладает тем свойством, что I состоит из всех ростков голоморфных функций, обращающихся в 0 на .В случае алгебраически замкнутого поля kэто равносильно тому, что слои 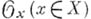пучка не содержат ниль-потентных элементов. Всякое гладкое пространство является приведенным. Если приведено, то можно считать, что состоит из ростков нек-рых непрерывных функций на X. Сечения пучка 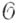па приведенном пространстве 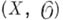отождествляются с аналлтич. ф-циями на , т. е. с аналитическими отображениями . Для произвольного А. п. имеется естественный эпиморфизм пучков (где (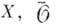 -приведенное А. п.), к-рый наз. приведением, или редукцией. Если - сечение пучка , то можно говорить о значении сечения в точке 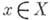(оно совпадает со значением аналитич. функции 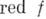в точке ). Поэтому алгебру ц в неприведенном случае часто наз. алгеброй аналитических (голоморфных) функций на . Пучки -модулей на А. п. наз. также аналитическими пучками.

Если 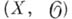- А. п., то каждое открытое определяет открытое подпространство 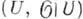. С другой стороны, можно ввести понятие аналитич. одпространства в 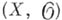, к-рое обязательно замкнуто. Множество наз. аналитическим, если в окрестности каждой точки оно определяется конечным числом аналитич. уравнений. С таким множеством связан пучок идеалов , состоящий из ростков всех аналитич. функций, равных 0 на Y. Обратно, каждый аналитический пучок идеалов конечного типа определяет аналитнч. множество Если , получается А. п. , к-рое наз. аналитическим подпространством в ; имеется естественный морфизм . Примером аналитич. одпространства в пространстве является его редукция.

Понятие А. п. возникло как обобщение понятия аналитич. многообразия. Такое обобщение подсказывала прежде всего алгебраич. геометрия, в к-рой уже давно систематически рассматривались пространства с особыми точками. Влияние идей алгебраич. геометрии непосредственно отразилось на окончательной формулировке понятия А. п. (для комплексных пространств в приведенном случае она была дана в [9], в общем случае - в [6]). В частности, каждая схема конечного типа над полным нормированным полем kестественным образом определяет А. п. над k. Это соответствие схем и А. п. над kдля приведенных комплексных пространств изучалось в [9], где теория А. п. была названа "аналитической геометрией". В дальнейшем обе геометрии развивались параллельно, причем обмен идеями между ними существенно способствовал успехам, достигнутым в обеих этих областях.

В теории функций многих комплексных переменных пространства с особыми точками возникли первоначально как римановы области, являющиеся аналогом римановых поверхностей функций одного переменного. Используя их в качестве локальных моделей, X. Венке и К. Штейн (Н. Behnke, K. Stein, 1951) определили нек-рый класс окольцованных пространств, к-рый, как показано в [5], совпадает с классом приведенных нормальных аналитических пространств. Локальная геометрия аналитич. множеств в С ⁿ была изучена еще В. Рюккертом (W.Ruckert) в l932.

Наконец, негладкие А. п. естественным образом возникают в теории автоморфных функций, как факторпространства аналитич. многообразий по собственным дискретным группам автоморфизмов. р-адические аналитич. множества появились впервые в работах Т. Сколема (Т. Scolem, 1935) в связи с нек-рыми задачами теории чисел.

Теория А. п. имеет два аспекта - локальный и глобальный. Локальная аналитич. еометрия рассматривает ростки аналитич. множеств в пространстве , снабженные пучками указанного выше вида. Основную роль здесь играет изучение свойств алгебры сходящихся степенных рядов от ппеременных над kи ее факторов - так наз. аналитич. алгебр, начало к-рому положил еще К. Вейерштрасс (К. Weierstrass). К локальной теории относятся теория нормализации, изучение особых точек, локальных свойств аналитич. функций и отображений и др. Основные результаты в этой области получены в случае, когда поле kалгебраически замкнуто (см. [1], [4], [7]). Здесь появляется важное понятие когерентного аналитического пучка, играющее далее ведущую роль в глобальной теории. В частности, структурный пучок А. п. и пучок идеалов любого аналитич. множества оказываются (в случае алгебраически замкнутого k).когерентными. Хорошо изучен также случай .

Глобальная аналитич. еометрия изучает свойства аналитич. функций, отображений и других аналитич. объектов, заданных "в целом" на всем А. п., а также геометрич. свойства этих пространств. В процессе изучения комплексных А. п. были выделены их естественные классы. Это прежде всего класс Штейна пространств, к-рый можно грубо охарактеризовать как класс пространств, обладающих достаточно большим запасом глобальных голоморфных функций. Пространства Штейна являются наиболее естественным многомерным обобщением областей комплексной плоскости, рассматриваемых в классич. теории функций одного комплексного переменного. Этот класс пространств по существу совпадает с классом аналитич. одпространств в пространствах СЩ. Его алгебраич. аналогом является класс аффинных алгебраич. многообразий (см. Аффинное многообразие).