Аппеля полином ы, - класс многочленов над полем комплексных чисел, содержащий многие классич. системы многочленов. А. м. введены П. Аппелем [1]. Последовательность А. м. 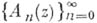определяется формальным равенством

в к-ром - формальный степенной ряд с комплексными коэффициентами причем . В явном виде А. м. A_n(z).выражаются через числа следующим образом:

Условие 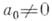равносильно тому, что степень многочлена равна .

Имеется другое, эквивалентное определение А. м. Пусть

- дифференциальный оператор, вообще говоря, бесконечного порядка, определенный над алгеброй Ркомплексных многочленов переменного Тогда

то есть представляет собой образ функции при отображении

Класс А. м. определяется как совокупность всевозможных систем многочленов с производящими функциями вида (1). Принадлежность системы многочленов (степени п).классу равносильна выполнению соотношений

Иногда при определении А. м. класса А ⁽¹⁾ пользуются соотношениями

к-рые, с точностью до нормировки, эквивалентны приведенным выше.

А. м. класса А ⁽¹⁾ используются при решении уравнений вида

формальное равенство 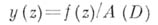при

позволяет записать решение (2) в виде

где 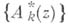- А. м. с производящей функцией В связи с этим особый интерес представляют разложения аналитич. функций в ряды по А. м. Кроме того, А. м. находят применение в различных задачах, относящихся к функциональным уравнениям, в том числе к дифференциальным уравнениям, отличным от (2), в вопросах интерполирования, теории приближения, в методах суммирования и др. (см., напр., [1] -[6]). С более общей позиции теория А. м. класса А ⁽¹⁾ (инек-рые приложения) изложена в [6].

А. м. класса А ⁽¹⁾ содержат в качестве частных случаев целый ряд классических последовательностей многочленов. Примерами, с точностью до нормировки, могут служить Бернулли многочлены

Эрмита многочлены

Лагерра многочлены

и т. д. Многочисленные примеры А. м. имеются в [2] и [3].

Существуют различные обобщения А. м., к-рые также носят назв. систем A.M. Сюда относятся А. м. с производящими функциями вида

а также А. м. с производящими функциями более общего характера:

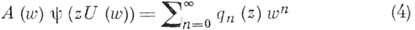
(см., напр., [2] и [3]). Если 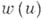- функция, обратная функции , то принадлежность системы многочленов к классу последовательностей А. м. с производящей функцией вида (3) равносильна выполнению соотношений

Имеется всего пять ортогональных с весом систем последовательностей А. м. на действительной оси, с производящими функциями вида (3); в том числе среди А. м. с производящими функциями вида (1) лишь одна система многочленов Эрмита является ортогональной с весом на действительной оси (см. [7]).

О разложениях в ряды по А. м. с производящими функциями вида (3) и (4), а также о связи этих А. м. с различными функциональными уравнениями см. [2], [7], [8].