приближение дифференциального уравнения и краевых условий системой конечных (обычно алгебраических) уравнений относительно значений искомой функции на нек-рой сетке, к-рое уточняется при стремлении параметра разностной задачи (шага сетки) к нулю.

Пусть требуется вычислить функцию и, принадлежащую линейному нормированному пространству функций, определенных в нек-рой области с границей Г, и являющуюся решением дифференциальной краевой задачи где 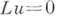-дифференциальное уравнение, -совокупность граничных условий. Пусть - сетка (см. Аппроксимация дифференциального оператора разностным).и - линейное нормированное пространство функции , определенных на этой сетке. Норма в вводится так, чтобы для любой функции 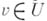выполнялось равенство

где - таблица значений функции vв точках сетки . Задачу вычисления решения изаменяют нек-рой задачей приближенного вычисления таблицы значений решения и в точках сетки . Здесь - нек-рая совокупность конечных (недифферен-циальных) уравнений относительно значений сеточной функции

Пусть - произвольная функция из и , - линейное нормированное пространство, к-рому принадлежат при любом Говорят, что задача является разностной аппроксимацией порядка рдифференциальной краевой задачи на решении последней, если

Фактическое построение системы 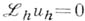разбивают на построение двух ее подсистем и В качестве 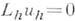используют к.-л. разностную аппроксимацию дифференциального уравнения (см. А п-проксимация дифференциального уравнения разностным). Дополнительные уравнения строят с использованием граничных условий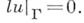

А. д. к. з. р. в смысле приведенного определения ни при каком выборе норм в 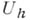и еще не обеспечивают сходимости (см. [2]) решения u_h разностной задачи к точному решению , т. е. равенства

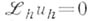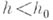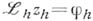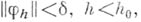Дополнительным условием, обеспечивающим сходимость, является свойство устойчивости (см. [3], [5] - [8]), к-рым должна обладать разностная задача . Задача наз. устойчивой, если существуют числа и такие, что уравнение имеет единственное решение при любом причем это решение удовлетворяет неравенству

где С- нек-рая постоянная, не зависящая от hи возмущения правой части , а - решение невозмущенной задачи . Если решение и дифференциальной задачи существует, а разностная задача аппроксимирует дифференциальную на решении ис порядком ри устойчива, то имеет место сходимость с тем же порядком, то есть

Напр., задача