- формула, выражающая число неподвижных точек эндоморфизма топологич. пространства через следы соответствующих эндоморфизмов в пространствах когомологий.

Эта формула была установлена впервые С. Лефшецом для конечномерных ориентируемых топологич. многообразий [1] и для конечных клеточных комплексов (см. [2, 3]). Этим работам С. Лефшеца предшествовала работа Л. Брауэра (L. Brouwer, 1911) о неподвижной точке непрерывного отображения га-мерной сферы в себя. Некоторый новый вариант доказательства Л. ф. для конечных клеточных комплексов был дан X. Хоп-фом (H. Hopf, см. [9]).

Пусть X - связное ориентируемое га-мерное компактное топологич. многообразие или га-мерный конечный клеточный комплекс, - непрерывное отображение, - Лефшеца число отображения f. Предполагается, что все неподвижные точки отображения изолированы. Для каждой неподвижной точки пусть i(х) - ее индекс Кронекера (локальная степень отображения f в окрестности точки х). Тогда Л. ф. для Xи fимеет вид

Имеется [8] обобщение Л. ф. на случай произвольных непрерывных отображений компактных евклидовых окрестностных ретрактов.

Пусть X - дифференцируемое компактное ориентированное многообразие, - дифференцируемое отображение. Неподвижная точка для отображения f наз. невырожденной, если она изолирована и 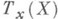- дифференциал отображения f в точке х,a E - тождественное преобразование. Для невырожденной точки ее индекс i(х).совпадает с числом sgn det (df_x-E). В этом случае Л. ф. (1) показывает, что число Лефшеца равно разности между числом неподвижных точек с индексом +1 и числом неподвижных точек с индексом -1, в частности не превосходит общего числа неподвижных точек. Левую часть формулы (1) в этом случае можно определить так же, как индекс пересечения на где Г _f - график отображения fи - диагональ.

Следствием Л. ф. является формула Хопфа, утверждающая, что эйлерова характеристика равна сумме индексов нулей глобального -векторного поля vна X(предполагается, что все нули векторного поля vизолированы) (см. [5]).

Существует вариант Л. ф. для компактных комплексных многообразий и когомологии Дольбо (см. [5]). Пусть X - компактное комплексное многообразие размерности ти - голоморфное отображение с невырожденными неподвижными точками. Пусть - когомологии Дольбо многообразия X типа ( р, q).и (X).- индуцированный отображением f эндоморфизм. Число

наз. голоморфным числом Лефшеца. Тогда имеет место следующая голоморфная

Л. ф.

где df_x - голоморфный дифференциал, отображения f в точке х.

В абстрактной алгебраич. геометрии Л. ф. послужила отправной точкой для поиска Вейля когомологии в связи с гипотезами Вейля о дзета-функциях алгебраич. многообразий, определенных над конечными полями. Аналог Л. ф. в абстрактной алгебраич. геометрии устанавливается для l-адических когомологии с компактными носителями и с коэффициентами в конструктивных -пучках, где - поле l-адических чисел, l- простое число, отличное от характеристики поля k. Эту формулу часто называют формулой следа.

Пусть X - алгебраич. многообразие (или схема) над конечным полем k, - морфизм Фробениуса и 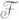- пучок на Xи - когомологии с компактными носителями многообразия (схемы) Xскоэффициентами в пучке Тогда морфизм Fопределяет эндоморфизм когомологии