Поиск по словарю Математический словарь
-
В закладки
 В закладки будет добавлено толкование к данному слову в данном словаре. Закладки сохраняются на Вашем компьютере в cookie. Если Ваш браузер не поддерживает cookie или такая возможность отключена, то сохранение закладок будет не возможно.
В закладки будет добавлено толкование к данному слову в данном словаре. Закладки сохраняются на Вашем компьютере в cookie. Если Ваш браузер не поддерживает cookie или такая возможность отключена, то сохранение закладок будет не возможно.Объемный Потенциал
- выражение вида
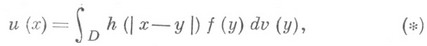
где D- конечная область евклидова пространства
 ограниченная замкнутой поверхностью (при N - 2- кривой) Ляпунова
ограниченная замкнутой поверхностью (при N - 2- кривой) Ляпунова  - фундаментальное решение оператора Лапласа,
- фундаментальное решение оператора Лапласа,
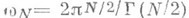 - площадь единичной сферы в
- площадь единичной сферы в  - расстояние между точками хи у,
- расстояние между точками хи у,  - элемент объема D.
- элемент объема D.Если
 то О. п. определен для всех
то О. п. определен для всех  . При этом в дополнительной области CD функция и(х)имеет производные всех порядков и удовлетворяет Лапласа уравнению
. При этом в дополнительной области CD функция и(х)имеет производные всех порядков и удовлетворяет Лапласа уравнению т. е. является гармонической функцией;при
т. е. является гармонической функцией;при  . эта функция регулярна на бесконечности,
. эта функция регулярна на бесконечности,  В области DО. п. и(х). принадлежит классу
В области DО. п. и(х). принадлежит классу  и удовлетворяет Пуассона уравнению
и удовлетворяет Пуассона уравнению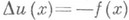 .
.Эти свойства обобщаются в различных направлениях. Напр., если
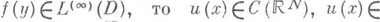
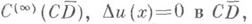 в Dсуществуют обобщенные производные 2-го порядка от и(х)и почти всюду в Dудовлетворяется уравнение Пуассона
в Dсуществуют обобщенные производные 2-го порядка от и(х)и почти всюду в Dудовлетворяется уравнение Пуассона  Изучены также свойства О. п. произвольной меры
Изучены также свойства О. п. произвольной меры  Радона, сосредоточенной на N-мерной области D:
Радона, сосредоточенной на N-мерной области D:
Здесь также

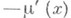 почти всюду в D. где
почти всюду в D. где  - производная меры m по мере Лебега в
- производная меры m по мере Лебега в  . В определении (*) фундаментальное решение оператора Лапласа можно заменить на произвольную функцию Леви для общего эллиптич. оператора 2-го порядка Lс переменными коэффициентами класса
. В определении (*) фундаментальное решение оператора Лапласа можно заменить на произвольную функцию Леви для общего эллиптич. оператора 2-го порядка Lс переменными коэффициентами класса 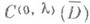 ; при этом перечисленные выше свойства остаются в силе с заменой
; при этом перечисленные выше свойства остаются в силе с заменой 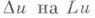 (см. [2]-[4]).
(см. [2]-[4]).О. п. применяется при решении краевых задач для эллиптич. уравнений с частными производными (см. При решении краевых задач для параболич. уравнений используется также понятие объемного теплового потенциала вида
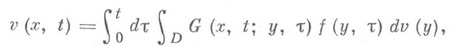
где
 - фундаментальное решение уравнения теплопроводности в
- фундаментальное решение уравнения теплопроводности в  :
:
 - плотность. Функция
- плотность. Функция 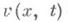 и ее обобщения на случай произвольного параболич. уравнения 2-го порядка имеют свойства, близкие к указанным выше для и(x)(см. [3] - [6]).
и ее обобщения на случай произвольного параболич. уравнения 2-го порядка имеют свойства, близкие к указанным выше для и(x)(см. [3] - [6]).Лит.:[1] Гюнтер Н. М., Теория потенциала и ее применение к основным задачам математической физики, М., 1953; [2] Миранда К., Уравнения с частными производными эллиптического типа, пер. с итал., М., 1957; [3] Тихонов А. Н., Самарский Л. А., Уравнения математической физики, 5 изд., М., 1977; [4] Смирнов В. И.. Курс высшей математики, 5 изд., т. 4, М., 1958; [5] Фридман А., Уравнения с частными производными параболического типа, пер. с англ., М., 1968; [6] Бицадзе А. В., Краевые задачи для эллиптических уравнений второго порядка, М., 196В.
Е. Д. Соломецев.