точки хотносительно группы G, действующей на множестве X(слева),- множество

Множество

является подгруппой в G и наз. стабилизатором, или стационарной подгруппой точки хотносительно G. Отображение индуцирует биекцию между G/G_x и орбитой G(x). О. любых двух точек из Xлибо не пересекаются, либо совпадают; иначе говоря, О. определяют разбиение множества X. Фактормножество по отношению эквивалентности, определенному этим разбиением, наз. пространством орбит, или фактормножеством X по G, и обозначается X/G. Сопоставление каждой точке ее О. определяет канонич. отображение . Стабилизаторы точек из одной О. сопряжены в G, точнее G_g(X)=gG_xg^-1. Если в Xимеется только одна О., то X - однородное пространство группы G; говорят также, что G действует на X транзит и вн о. Если G - топологич. группа, X - топологич. пространство и действие непрерывно, то X/G обычно снабжается топологией, в к-рой множество открыто в X/G тогда и только тогда, когда множество открыто в X.

Примеры. 1) Пусть G - группа поворотов плоскости Xвокруг фиксированной точки а. Тогда О.- это всевозможные окружности с центром в а (в том числе и сама точка a). 2) Пусть G - группа всех невырожденных линейных преобразований конечномерного действительного векторного пространства V, X - множество всех симметрич. билинейных форм на V, а действие G на Xопределено формулой (gf)(u, v)=f(g^-1(u), g^-1(v)).для любых и, . Тогда О. группы G на X -множество форм, имеющих фиксированный ранг и сигнатуру.

Пусть G - вещественная группа Ли, гладко действующая на дифференцируемом многообразии X(см. Ли группа преобразований). Для любой точки 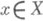орбита G(x).является погруженным подмногообразием в X, диффеоморфным G/G_x (диффеоморфизм индуцирован отображением . Это подмногообразие не обязательно замкнуто в X(не обязательно вложено). Классич. примером служит "обмотка тора", то есть О. действия аддитивной группы на торе

заданного формулой

где a - иррациональное действительное число; замыкание такой О. совпадает с T². Если G компактна, то все О. являются вложенными подмногообразиями.

Если G - алгебраич. группа, X - алгебраич. многообразие над алгебраически замкнутым полем k,a действие регулярно (см. Алгебраическая группа преобразований), то любая орбита G(x).является гладким алгебраич. многообразием, открытым в своем замыкании (в топологии Зариского), причем в всегда содержится замкнутая О. группы G (см. [5]). В этом случае морфизм индуцирует изоморфизм алгебраич. многообразий G/G_x и G(x).тогда и только тогда, когда он сепарабелен (это условие всегда выполнено, если k - поле нулевой характеристики). О. максимальной размерности образуют открытое в Xмножество.

Описание структуры О. для данного действия обычно сводится к указанию в каждой О. нек-рого единственного представителя х, к нахождению стабилизатора G_x и к описанию какого-либо - по возможности обозримого - класса функций, постоянных на О. (инвариантов) и разделяющих разные О.; эти функции позволяют описать "расположение" О. в X (О. являются пересечениями их множеств уровня). Эта программа обычно наз. задачей орбитального разложения. К такой задаче часто сводятся многие задачи классификации. Так, в примере 2) это - задача классификации билинейных симметрич. форм с точностью до эквивалентности; инварианты в этом случае "дискретны" - это ранг и сигнатура, а стабилизатор G_f, где f невырождена, является соответствующей псевдоортогональной группой. Классич. теория жордановой формы матриц (также, как и теории других нормальных форм матриц) тоже укладывается в эту схему: жорданова форма - это канонич. представитель (определенный, правда, с точностью до порядка жордановых клеток) в О. полной линейной группы GL_n(C) на пространстве всех комплексных (nХn)-матриц при действии, заданном формулой ; среди инвариантов важное место занимают коэффициенты характеристич. многочлена матрицы Y(к-рые не разделяют, однако, любые две О.). Идея рассмотрения эквивалентных объектов как О. нек-рой группы активно используется в различных задачах классификации, напр. в алгебраич. модулей теории (теория Мамфорда, см. [10]), в теории перечисления графов (см. [2]) и др. Если Gи X конечны, то

где |Y| - число элементов множества Y, а

Если G - компактная группа Ли, гладко действующая на связном гладком многообразии X, то структура О. на Xлокально конечна, т. е. у любой точки существует такая окрестность U, что число различных стабилизаторов , с точностью до сопряженности в Gконечно. В частности, если Xкомпактно, то конечно число различных (с точностью до сопряженности в G).стабилизаторов . При этом для любой подгруппы H в G каждое из множеств

Х (Н) = {сопряжена Нв G}