гауссовский стационарный случайный процесс V(t).с нулевым математич. ожиданием и экспоненциально затухающей корреляционной функцией вида

О. - У. п. может быть также определен как стационарное решение стохастич. уравнения (уравнения Ланжевена) вида

где W(t) - винеровский процесс (так что =W'(t) - обобщенный случайный процесс белого шума), a m и b - положительные постоянные, причем b/m=a.

Уравнение (*) приближенно описывает одномерное броуновское движение свободной частицы; при этом V(t).интерпретируется как скорость частицы, т- ее масса, - bV (t) - пропорциональная скорости сила "вязкого трения" (для сферич. частицы радиуса акоэффициент b равен 6pha, где h) - коэффициент вязкости, в силу гидродинамич. формулы Стокса), а белый шум W'(t) - это "случайная сила", порожденная хаотич. толчками молекул среды, находящихся в тепловом движении, и являющаяся основной причиной броуновского движения. В первоначальной теории броуновского движения, развитой А. Эйнштейном (A. Einstein) и М. Смолуховским (М. Smoluchowski) в 1905-06, пренебрегалось инерцией частицы, т. е. считалось, что m=0; при этом уравнение приводило к выводу, что координата броуновской частицы

равна b^-1W(t), т . е. представляет собой винеровский процесс. Таким образом, винеровский процесс описывает модель Эйнштейна - Смолуховского броуновского движения (отсюда другое его название - процесс броуновского движения); т. к. этот процесс недифференцируем, то в теории Эйнштейна - Смолуховского частица, совершающая броуновское движение, не имеет конечной скорости. Уточненная теория броуновского движения, опирающаяся на уравнение.

, где , была предложена Л. Орнштейном и Дж. Уленбеком ([1]; см. также [2]); позже та же теория была выдвинута С. Н. Бернштейном [3] и А. Н. Колмогоровым [4]. В теории Орнштейна - Уленбека скорость V(t).броуновской частицы является конечной, но ее ускорение бесконечно (так как О.- У. п. недифференцируем); для того чтобы и ускорение оказалось конечным, надо уточнить теорию, учтя отличие случайной силы от идеализированного белого шума W'(t).

Уравнение можно использовать и для описания одномерного броуновского движения гармонич. осциллятора, если пренебречь его массой и считать, что

V(t) - это координата осциллятора, - сила вязкого трения, -bV - регулярная упругая сила, удерживающая осциллятор, a W'(t).- случайная сила, создаваемая молекулярными толчками. Таким образом, О.- У. п. доставляет также модель пульсаций координаты гармонич. осциллятора, совершающего броуновское движение, родственную модели Эйнштейна - Смолуховского броуновского движения свободной частицы.

О.- У. п. является однородным по времени марковским процессом диффузионного типа (см. Диффузионный процесс);наоборот, процесс V(t), являющийся одновременно стационарным случайным процессом, гауссовским процессом и марковским процессом, обязательно представляет собой О.- У. п. Как марковский процесс О.- У. п. удобно характеризовать его переходной плотностью вероятности р(t, x, у), представляющей собой фундаментальное решение соответствующего уравнения Фоккера - Планка (т. е. прямого Колмогорова уравнения).вида

и, следовательно, задаваемой формулой

Многие свойства О.- У. п. V(t).(включая и его марковость) можно вывести из известных свойств винеровского процесса, воспользовавшись тем, что процесс

является стандартным винеровским процессом (см. [5]). В частности, отсюда следует, что реализации О.- У. п. непрерывны и нигде не дифференцируемы с вероятностью 1 и что

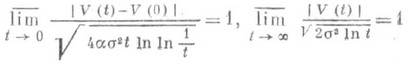
с вероятностью 1.

Лит.:[1] Uhlenbесk G. Е., Оrnstein L. S., "Phys. Rev.", 1930, v. 36, p. 823-41; [2] Чандрасекар С., Стохастические проблемы в физике и астрономии, пер. с англ., М., 1947; [3] Бернштейн С. Н., "Докл. АН СССР", 1934, т. 1, № 1,с. 1-9; № 7, с. 361-65; [4] Ко1mоgоrоv A. N.,"Ann. Math.", 1934, v. 35, p. 116 - 17; [5] Doob J. L., "Ann. Math.", 1942, v. 43, p. 351 - 69. А. M. Яглом.

OPPA - ЗОММЕРФЕЛЬДА УРАВНЕНИЕ - линейное обыкновенное дифференциальное уравнение

где R- число Рейнольдса, w(y).- заданная функция (профиль скорости невозмущенного потока), к-рая обычно предполагается голоморфной в окрестности отрезка [-1, 1] в комплексной плоскости y, a>0 - постоянная и с - спектральный параметр. Для О.- 3. у. исследуется краевая задача