ряд вида

где - ортонормированная система функций (онс) относительно меры :

Начиная с 18 в. при изучении различных вопросов математики, астрономии, механики и физики (движение планет, колебание струн, мембран и др.) в исследованиях Л. Эйлера (L. Euler), Д. Бернулли (D. Bernoulli), А. Лежандра (A. Legendre), П. Лапласа (Р. Laplace), Ф. Бесселя (F. Bessel) и др. эпизодически появляются нек-рые специальные онс и разложения функций по ним. Определяющее же влияние на становление теории О. р. оказали:

а) исследования Ж. Фурье (J. Fourier, 1807-22) (Фурье метод решения краевых задач уравнений математич. физики) и в связи с ними работы Ж. Штурма и Ж. Лиувилля (J. Sturm,. J. Liouville, 1837-41);

б) исследования П. Л. Чебышева по интерполированию и проблеме моментов (сер. 19 в.), повлекшие за собой создание им общей теории ортогональных многочленов;

в) исследования Д. Гильберта (D. Hilbert, нач. 20 в.) по интегральным уравнениям, где, в частности, были установлены общие теоремы о разложении функций в ряд по онс;

г) создание А. Лебегом (Н. Lebesgue) теории меры н интеграла Лебега, придавшие теории О. р. современный вид.

Активному развитию теории О. р. в 20 в. способствует применение онс функций и рядов по ним в самых разнообразных разделах науки (математич. физика, вычислительная математика, функциональный анализ, квантовая механика, математич. статистика, операционное исчисление, автоматич. регулирование и управление, различные технич. задачи и т. п.).

Характерные результаты и направления исследований в теории О. р.

1) Пусть - мера Лебега и {j_n} - онс. Тогда если , то числа

наз. коэффициентами Фурье, а ряд (1) с - рядом Фурье функции f по системе

Система замкнута относительно пространства L², если для любой функции и любого числа найдется полином

такой, что норма . Система полна относительно L², если из условий и a_n(f)=0 при всех следует, что f(x)=0 почти всюду, т. е. f - нулевой элемент пространства L²

Если для нек-рой функции 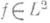выполняется равенство

(2)

то говорят, что функция f удовлетворяет условию замкнутости Ляпунова - Стеклова (или равенству Парсеваля). Это условие эквивалентно сходимости частных сумм ряда Фурье от f по норме пространства L² к функции f.

Аналогично даются определения замкнутости, полноты и условия замкнутости для более общих пространств и мер.

Одним из важнейших вопросов теории О. р. является вопрос однозначного определения функции по ее коэффициентам Фурье. Для пространств L² он самым тесным образом связан с выполнением равенства (2) для всех функций

Для случая тригонометрич. системы равенство (2) в 1805 было приведено (фактически без доказательства) М. Парсевалем (М. Parseval), а в 1828 Ф. Бессель установил, что

неравенство Бесселя). В 1896 А. М. Ляпунов доказал равенство (2) для интегрируемых по Риману функций, а потом П. Фату (P. Fatou) для случая

В. А. Стекловым (1898-1904) был поставлен вопрос о замкнутости общих онс и положительно решен для многих ортогональных систем (сферич. функции, собственные функции оператора Штурма - Лиувилля, системы ортогональных многочленов Эрмита, Лагерра, функции Ламе и др.).

Что касается неравенства (3), то оно оказалось справедливым для произвольных онс и функций

С 1907 Ф. Рисс (F. Biesz) и Э. Фишер (Е. Fischer) доказали, что для любой онс 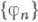и любой последовательности чисел найдется функция , для к-рой и выполнено равенство (2). Из этой теоремы и неравенства Бесселя вытекает, что для любых онс полнота и замкнутость эквивалентны в пространстве L²;замкнутость в пространствах L^p с эквивалентна полноте в пространстве L^p', где (С. Банах, S. Banach, 1931).

Неравенство Бесселя и теорема Рисса - Фишера были распространены Г. Харди (G.'Hardy), Дж. Литлвудом (J. Littlewood) и Р. Пэли (R. Paley) на пространства L^p. Именно, пусть - онс, и . Тогда:

а) если , то

б) если дана последовательность с

то найдется функция , для к-рой и , где Азависит лишь от ри М.

2).Другой крупной проблемой теории О. р. является вопрос разложения функции в ряд по простым функциям, сходящийся к ней по норме того пли иного пространства. Система элементов из B-прост-ранства Енал. базисом (безусловным базисом), если каждый элемент 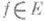единственным образом представляется в виде ряда

сходящегося (безусловно сходящегося) к f по норме пространства Е.

Если 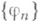- базис в Е, то являются линейными непрерывными функционалами в пространстве Еи в случае с имеют вид

где - базис пространства

биортонормированная система (С. Банах). В частности, если , то есть - онс, то ортого-

нальный базис в L^p автоматически является базисом во всех пространствах L^r, где r- любое число между pи р'.

Исследования по указанной проблеме ведутся в двух направлениях:

а) по заданной онс находятся те пространства, в к-рых является базисом;

б) для заданного пространства Еотыскиваются в нем базисы или ортогональные базисы.

В обоих случаях исследуется взаимосвязь свойств функции f и ее разложения.

Что касается тригонометрич. системы, то она не является базисом пространства непрерывных функций С(П. Дюбуа-Реймон, P. Du Bois Reymond, 1876), но является базисом в пространствах L^p с (М. Рисc, М. Riesz, 1927). Результат П. Дюбуа-Реймона был распространенна любые ограниченные в совокупности онс.

Ортонормированная система многочленов Лежандра является базисом в пространствах L^p при и не является таковой в остальных пространствах L^q(1946-52, X. Поллард, H. Pollard, Дж. Нейман, J. Neumann, и В. Рудин, W. Rudin).

В 1910 была построена онс такая, что всякая непрерывная функция единственным образом раскладывается в равномерно сходящийся ряд Фурье по этой системе (А. Хаар, А. Нааr). Однако система Хаара не является базисом пространства С(0,1), т. <к. функции=""> разрывны при . Проинтегрировав систему , Г. Фабер (G. Faber, 1910) установил, что система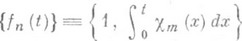

является базисом в пространстве С(0,1) и тем самым был найден первый базис в пространстве непрерывных функций. Этот результат Г. Фабера был переоткрыт Ю. Шаудером (J. Schauder, 1927), к-рый указал также класс базисов пространства С(0,1) типа базиса ; в честь последнего и введен термин "базис Шаудера", хотя более справедливо было бы называть его "базис Фабера - Шаудера".

Построенные Г. Фабером и Ю. Шаудером базисы не являются ортогональными. Первый ортонормированный базис {F_n} в пространстве С (0,1) был найден Ф. Франклином (Ph. Franklin, 1928), к-рый проортогонализировал методом Шмидта систему Фабера - Шаудера {f_n} и получил {F_n}. На этом пути (ортогонализация и интегрирование) был введен и изучен новый класс базисов. Все ортонормированные базисы пространства С(0,1) автоматически являются базисами во всех пространствах L^p с

Система Хаара является безусловным базисом но всех пространствах L^p с (1931-37, Р. Пэли, Ю. Марцинкевич, J. Marcinkiewicz). Аналогичный результат имеет место и для системы {F_n} Франклина.