- раздел комплексного анализа, изучающий вопросы приближенного представления (аппроксимации) функций комплексного переменного посредством аналитич. ций специальных классов. Основными в теории П. ф. к. п. являются задачи о возможности приближения, скорости приближения и об аппроксимационных свойствах различных способов представления функций (интерполяционных последовательностей и рядов, рядов по ортогональным многочленам и многочленам Фабера, разложений в непрерывные дроби и аппроксимаций Паде, последовательностей полиномов из экспонент и рядов Дирихле и т. п.). Теория П. ф. к. п. тесно связана с другими разделами комплексного анализа и математики в целом; в теории приближений важную роль играют методы и результаты конформных отображений, интегральные представления, теория потенциала, теория функциональных алгебр и др.

Центральная проблематика теории П. ф. к. п. относится к приближению функций многочленами и рациональными функциями, в частности многочленами и рациональными функциями наилучшего приближения (существование, характеристич. свойства, единственность), а также экстремальные задачи и различные оценки для многочленов и рациональных функций (оценки роста, неравенства для производных, многочлены и рациональные функции, наименее уклоняющиеся от нуля, и т. <п.).> А. А. Гончар.

Приближение функций комплексного переменного многочленами и рациональными функциями. В этом разделе теории П. ф. к. п. можно выделить несколько направлений.

1) Изучение возможности приближения функции f(z) комплексного переменного z с любой наперед заданной точностью посредством многочленов и рациональных функций от z в зависимости от свойств того множества Е, на к-ром задана f и на к-ром происходит приближение, от свойств метрики уклонения r и, наконец, от свойств самой функции f.

2) Изучение свойств многочленов и рациональных функции наилучшего приближения, т. е. таких многочленов Р _п(z; f, E,r) и рациональных функций R_n(z; f, Е,r).степени не выше и, n=0, 1, ... , для к-рых

где нижние грани берутся соответственно по всем многочленам Р(z) степени deg Pпи рациональным функциям R(z) степени deg R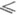п(либо по части множества таких многочленов или рациональных функций, выделяемой какими-либо дополнительными условиями). По существу здесь идет речь о свойствах решений нек-рого класса экстремальных задач. Сюда можно отнести также изучение и других экстремальных задач на множествах многочленов, рациональных функций и на нек-рых классах аналитич. ций, а также исследования аналитич. свойств многочленов и рациональных функций (в частности, получение неравенств между различными нормами этих функций и их производных).

3) Изучение зависимости скорости убывания к нулю величин E_n(f, Е,r) и R_n(f, E,r) при от свойств f, Еи r (так наз. прямые теоремы теории приближения) и зависимости свойств функции f от скорости убывания E_n(f, Е,r) или R_n(f, Е,r) к нулю при и свойств E и r (обратные теоремы). С этим направлением неразрывно связано изучение возможностей известных методов П. ф. к. и. (таких, как ряды по Фабера многочленам, различные интерполяционные процессы и т. п.) и отыскание новых эффективных методов приближения.

4) Приближение функций нескольких комплексных переменных. Здесь решаются в основном те же задачи, что и в случае одного переменного, однако результаты и методы их получения, как правило, резко отличаются от случая одного переменного.

Ниже отмечены нек-рые основные результаты.

1) Задачу о возможности сколь угодно хорошего равномерного приближения многочленами решают Рунге теорема (в случае аналитичности f на Е), Лаврентьева теорема (непрерывность f на Е), Келдыша теорема( Е - замкнутая область, f непрерывна на Еи аналитична внутри Е), Мергеляна теорема (в общем случае: Е- компакт, f непрерывна на Еи анаяитична во внутренних точках Е).

2) Задачу о возможности приближения голоморфной функции на замкнутом подмножестве Ерасширенной комплексной плоскости решает теорема Рунге. При изучении возможности приближения функций f из различных пространств в метрике этих пространств посредством рациональных функций важную роль играют количественные характеристики множеств , аналогичные аналитической емкостиg(е). В терминах g(е).задача об описании компактов Е, на к-рых любая непрерывная функция с любой точностью приближается рациональными функциями, решается следующим образом: необходимо и достаточно выполнение либо условия

(а)

для любого круга либо условия

(б) для любого (эквивалентность условий (а) и (б) выражает т. н. "неустойчивость" аналитической емкости).

3) Если Еограничено и измеримо йо Лебегу и 1р<2, то множество всех рациональных функций плотно в пространстве L^p(E).

4) Если р>0, G - односвязная область с жордановой спрямляемой границей, то семейство всех многочленов от z плотно в Смирнова классе E_p(G).тогда и только тогда, когда G - Смирнова область.

5) Пусть комплекснозначные функции (j₁(z), ... , j_n(z), f(z) непрерывны на компакте . Среди всех обобщенных полиномов вида

( с ₁, ... , с _n - произвольные комплексные числа) обобщенный полином P₀(z).является наименее уклоняющимся от f по метрике

тогда и только тогда, когда

для каждого P(z).