общее название Класса распределений вероятностей, возникающего при распространении идеи "равновозможности исходов" на непрерывный случай. Подобно нормальному распределению Р. р. появляется в теории вероятностей как точное распределение в одних задачах и как предельное - в других.

Р. р. на отрезке числовой прямой (прямоугольное распределение). Р. р. на каком-либо отрезке [ а, b], а<b, - это распределений вероятностей, имеющее плотность

Понятие Р. р. на [ а, b] соответствует представлению о случайном выборе точки на этом отрезке "наудачу". Математич. ожидание и дисперсия Р. р. равны, соответственно, (b+a)/2 и (b-а)²/12. Функция распределения задается формулой

а характеристич. функция - формулой

Случайную величину с Р. р. на [0,1] можно построить, исходя из последовательности независимых случайных величин Х ₁, Х ₂, . . ., принимающих значения 0 и 1 с вероятностями ¹/₂ полагая

( Х _n являются цифрами в двоичном разложении X). Случайное число Xимеет Р. р. на отрезке [0,1]. Этот факт имеет важные статистич. приложения, см., напр., Случайные и псевдослучайные числа.

Если независимые случайные величины Х ₁ и Х ₂ имеют Р. р. на [0,1], то их сумма Х ₁+Х ₂ имеет так наз. треугольное распределение на [0,2] с плотностью u₂ (х)=1 -|1-х | для и u₂(x)=0 для . Сумма трех независимых случайных величин с Р. р. на [0,1] имеет распределение на [0,3] с плотностью

В общем случае сумма X₁+X₂+. . . +Х _n независимых величин с Р. р. на [0,1] распределена с плотностью

для и и _п (х)=0 для ; здесь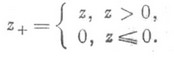

Распределение суммы нормированной математич. ожиданием n/2 и среднеквадратич. отклонением , с ростом пбыстро сближается с нормальным распределением с параметрами 0 и 1 (уже при n=3 приближение удовлетворительно для многих практич. целей).

В статистич. приложениях процедура построения случайной величины с заданной функцией распределения F(х).основана на следующем факте. Пусть случайная величина Yраспределена равномерно на [0,1] и функция распределения F(х).непрерывна и строго возрастает. Тогда случайная величина имеет функцию распределения F(х).(в общем случае надо заменить в определении Xфункцию F^-1 (у).на нек-рый ее аналог, а именно ).

P.p. на отрезке как предельное распределение. Ниже приводятся типичные примеры возникновения Р. р. на [0,1] в качестве предельного.

1) Пусть X₁, X₂, . . ., Х _n,... - независимые случайные величины, имеющие одну и ту же непрерывную функцию распределения. Тогда распределение их суммы S_n, приведенной по mod 1, т. е., иными словами, распределение дробной части {S_n} суммы S_n, сходится к равномерному на [0, 1] распределению.

2) Пусть параметры и имеют абсолютно непрерывное совместное распределение; тогда при распределение сходится к равномерному на [0,1].

3) Р. р. встречается как предельное распределение дробных долей нек-рых функций g(n) натурального аргумента п. Напр., при иррациональном a. доля тех , из пдля к-рых

имеет пределом при величину b-а.

Р. р. на под множествах . Пример Р. р. в прямоугольнике встречается уже в Бюффона задаче (см. также Геометрические вероятности, Стохастическая геометрия]. Р. р. на нек-ром ограниченном множестве Dв евклидовом пространстве определяется как распределение, имеющее плотность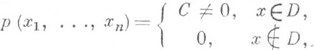

где Собратна k-мерному объему (или лебеговой мере) области D.

Рассматривают также и Р. р. на поверхностях. Так, "случайное направление" (напр., в ) определяют вектором, идущим из начала координат в случайную точку поверхиости единичной сферы, равномерно распределенную в том смысле, что вероятность ее попадания в какую-либо часть поверхности пропорциональна площади этой части.

Роль Р. р. на алгебраич. группах играет нормированная Хаара мера.

Лит.:[1] Феллер В., Введение в теорию вероятностей и ее приложения, пер. с англ., 2 изд., т. 2, М., 1967.

А. В. Прохоров.